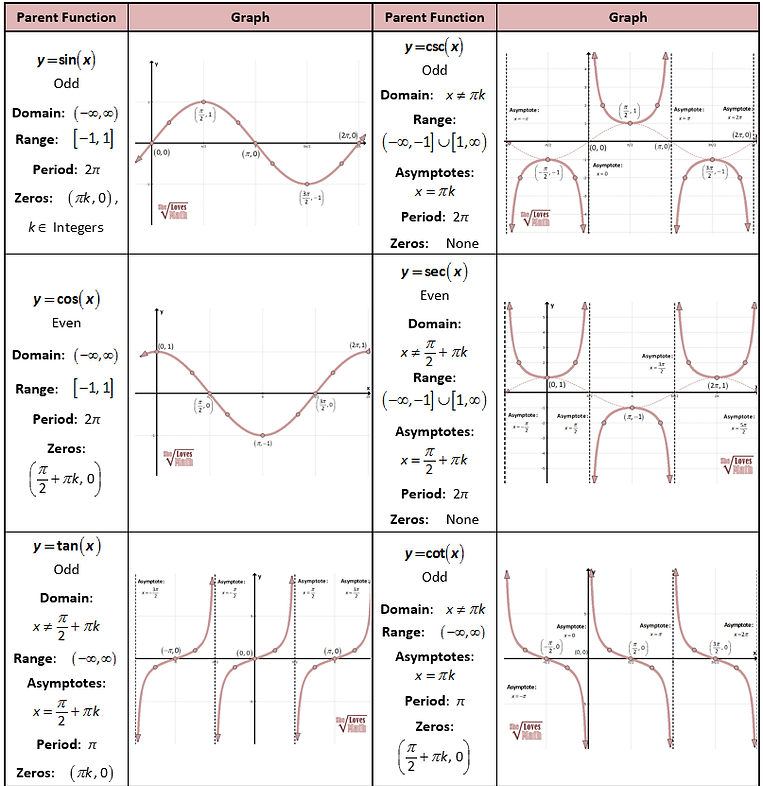
6.5 Exploring Graphs Of The Reciprocal Trigonometric Functions
Helpful Videos
When investigating the graphs of reciprocal trigonometric functions, it is important to note that their graphical characteristics are specifically related to those of primary trig functions. This is because reciprocal trigonometric functions are defined as the following:
YOU TRY! Using graphing technology, such as the online graphing calculator provided below, graph these reciprocal trigonometric functions on the same set of axis as the primary trigonometric functions.
You should observe the three graphs on the left.
The graphs of reciprocal functions have vertical asymptotes at the zeroes of their primary trigonometric functions.
This is because the primary trigonometric functions are the denominators of the fractions that make up the reciprocal function. Since the denominator can never equal zero (or else the function will become undefined) there must be vertical asymptotes.
For the cosecant function, there are asymptotes wherever the function of sine has a y-value of zero. For the secant function, there are asymptotes wherever the function of cosine has a value of zero. For the cotangent function, the asymptotes occur where the value of the tangent function has a value of zero, or in other words wherever the sine function has a value of zero.
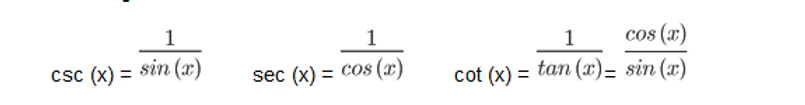
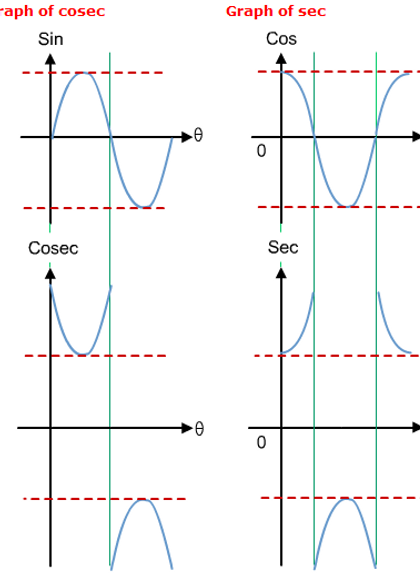
Additionally, for cosine and sine functions, the minimum and maximum points are where the graphs interact with the graphs of their reciprocal functions. Wherever a primary function has a local maximum, the reciprocal function will have a local minimum and vice versa.
Sample Questions
Level 1/2
Compare the graphs of y = cscx and y = secx and include descriptions of the following properties: period, equation of axis, amplitude, max. and min values and domain.
Level 3
A) Find an expression which describes the location of vertical asymptotes for y = csc (x), y = sec (x) and y = cot (x), where n is an element of I?
A) If y = sin(x) undergoes a shift to the left by then its graph is the same as cos (x). Is the same true for graphs of y = csc (x) and y = sec (x)? Why or why not?
Key Concepts