
7.5 Solving Linear Trigonometric Equations
Helpful Videos
For 0 < x < 2π Solve for 2cos(x) - 1 = 0
Example 1
Step 1) Rearrange equation so terms containing a trigonometric funtion is one one side and the constants/numbers on the otherside (for linear equation)
Step 2) Rearrange so that the trigonometric function is by itself
Step 3) Now that you have solved that cos(x) = 1/2 find the solutions in the interval using the unit circle which in this question is 0 < x <2π.
NOTE: Be mindful that the sign of the value determines which quadrants the solution will occur in.
2cos(x) - 1 = 0
2cos(x) = 1
cos(x) = 1/2
Since cos is + the solutions are in quadrants 1 & 4
cos(x) = 1/2 at 60 and 300 degrees or π/3, 5π/3
For 0 < x < 2π Solve for 7cos(x) + √3 = 5cos(x)
Example 2

There are different types of linear and quadratic trigonometric equations. Just like the normal quadratic or linear functions these trigonometric functions have sin, cos, tan, cot..ect as a part of the equation.
What is the difference between:
Y = 4x + 6
Y = 4cos(x) + 6 or Y= 4sin(x) +6
Solving these equations is almost identical to solving normal quadratic or linear functions.
This means isolating x or in this case your sin, cos, tan..ect
Which can be achieved by factoring out common factors using the FOIL method and in some cases using methods such as the quadratic formula.
After isolating the variables, using the unit circle we can evaluate where on the unit circle these values. However there are some restrictions such as the value for x or sin(x) for example cannot be more than 1 or less than -1 because you know that these are both defined as the maximum and minimum value for this specific trigonometric function and values not within this range are not part of the function. We can use the related acute angle to find other solutions in an interval when the value has been found.
NOTE: Identities and equations are different, identities are true for all values of x in a given domain but equations are true in only some cases, therefore is not defined as an identity.
Real life applications pertaining to trigonometric equations include uses by oceanographers to measure the height of tides in oceans, and properties of sound waves. A specific application is camera lens filters such as the ones in LCD TVs which is used to reduce light intensity for your eyes. This specif application is modelled as I=Iocos^2(x) where Io represents the intensity of the initial beam of light and I is the intensity from the polarizing material.

Step 1) Rearrange equation so terms containing a trigonometric funtion is one one side and the constants/numbers on the otherside (for linear equation)
Step 2) Rearrange so that the trigonometric function is by itself
Step 3) Now that you have solved that cos(x) = -√3 /2 find the solutions in the interval using the unit circle which in this question is 0 < x <2π.
NOTE: Be mindful that the sign of the value determines which quadrants the solution will occur in.
7cos(x) + √3 = 5cos(x)
cos(x) = -√3 /2
Since cos is - the solutions are in quadrants 2 & 3
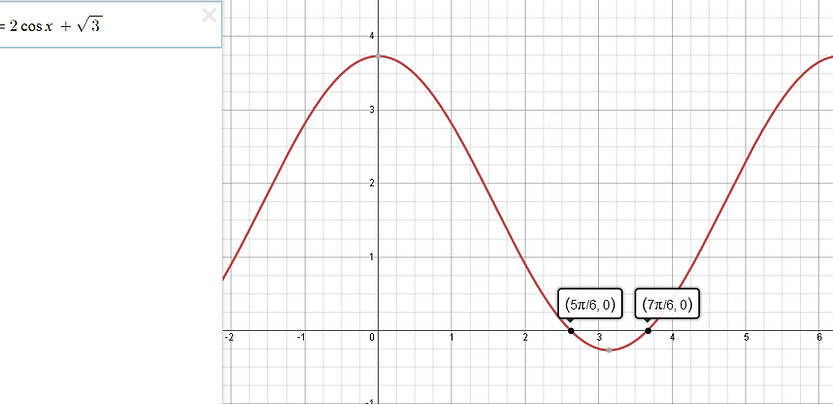
cos(x) = -√3 /2 at 150 and 210 degrees or 5π/6, 7π/6
7cos(x) - 5cos(x) + √3 = 0
2cos(x) = -√3
Method 2: Graphing
1) You can solve linear equations by graphing the function and finding the x values will tell you what the solutions are
Sample Questions
Level 1/2
A) For 0 < x < 2π Solve for sin(x)= - √3/2
B) For 0 < x < 2π Solve for sin(x) = - 0.4563
C) For 0 < x < 2π Solve for cos(x) = √2/2
Level 3 (Application)
There is a model that represents a islands daily temperature modelled by a cosine function amplitude of -30 a period of 2π/365 and a equation of axis of 5 Where d is the day of the year. What is the first day of the year where the temperature is below 0 degrees?
Key Concepts/Tips
Due to their periodic nature trigonometric equations have infinite solutions so intervals are used in these models to find specifc solutions.
Special angles, Calculators, Graph sketching/ CAST rule are all strategies that can be used to solve trigonometric equations.
Use the related acute angle to help determine all the cooresponding solutions in the given interval.
To use the graphing method you can verify the solutions by:
graphing the appropriate functions on the graphing calculator and determining the point of intersection
Graphing a single equivalnet function and determining its zeroes.