
6.6 Modelling Trigonometric Functions
Helpful Videos
Ex. Once every year, the tides at a beach in Miami, Florida occur in record-breakingly short cycles of 6 hours. The first low tide was measured at a height of 3.4 m at 12 A.M. and the first high tide was measured at a height of 11.7 m at 3 A.M. Determine an equation which models this function.
When modelling a trigonometric function, we are simply trying to coordinate aspects of the questions to variables of the standard equation.
This may sound confusing, but there is a basic structure to follow when doing this.
Before you set out to find the equation, it is important to first decide whether the situation is better modelled by a sine or cosine function. If it seems like the function starts a maximum or minimum value, it is more appropriate to use a cosine function instead of a sine function shifted and vice versa.
Example 1
Since we are starting at a minimum, a cosine model is appropriate.
The amplitude can be found by adding the maximum and minimum value and dividing by two. The low tide represents the minimum height and the high tide represents the maximum height.
a = [11.7 - 3.4]/2 = 8.3/2 = 4.15
Therefore the amplitude is equal to 4.15.
The c value, the equation of the axis, can be found adding the maximum (high tide) and minimum (low tide) heights and dividing by two.
c = [11.7 +3.4]/2 = 15.1/2 = 7.55
Therefore the equation of the axis is equal to 7.55.
The k value can be found by dividing 2π by the period. The period is the time it takes to complete one cycle. In this case, each cycle lasts 6 hours. Therefore, the period must be 6 hours.
k = 2π/6= π/3(simplifed the fraction)
Therefore the k-value is equal to π/3.
Therefore y = - 4.15 cos(π/3x) + 7.55
Step 1) Figure out which function models the situation the best. Use knowledge of maximum and minimum values to evaluate your choices.
Step 2) Use maximum and minimum values to determine your amplitude as well as you equation of axis.
Step 3) Determine your period by dividing 2π by your k value
Step 4) Put all these elements together, you should produce the equation that models this periodic relationship.
NOTE: Since the function is starting at a minimum value and we chose to use a cosine model, we don’t require a phase shift. However, there should be a flip across the x-axis (since cosine functions usually start a maximum).
In this part of the chapter, we learn how to apply trigonometric functions to real life situations. What does an amplitude actually mean? And a period?
Let us first take a look at the standard equation of a trigonometric function:
y = a sin [k(x-d)] + c
In the transformations part of this chapter (see 6.4 Transformations of Trigonometric Functions), we learned what each of these variables meant.
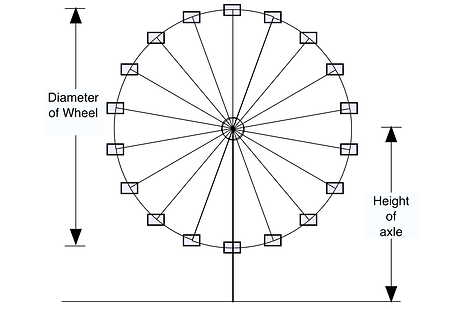
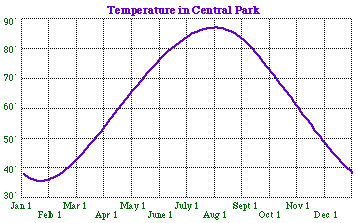
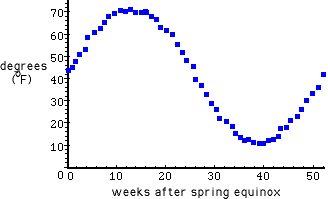
When trying to determine the amplitude of the equation, simply subtract the minimum value from the maximum value and divide by two.
Usually the period will be provided and you will be required to determine the k-value, which can be done by using the following formula: period = 2πk. If you already know the period. To find the k-value, all you need to do is divide 2π by the period.
The c variable, which represents the equation of the axis, can be determined by taking the sum of the maximum and minimum values and dividing it by two.
The d variable, the phase shift, can be found by subbing in the above variables along with another point (most likely a minimum or maximum value) and isolating d. (Most of the time, though, there is not really a phase shift.)
The best way to really grasp these concepts is to try it yourself! Check out the tutorial below which shows you how to approach these types of questions.
Sample Questions
Level 1/2
1. A sinusoidal curve starts a minimum. It has a period of 4 radians and a horizontal shift of 3. It’s maximum value is 26 and it’s minimum value is 4. Determine the equation that models this curve.
Level 3 (Application)
As a guy crosses the street, he swings his keychain in a circular motion at a constant speed. The keys move in a plane that is perpendicular to the ground.
A) What does the amplitude mean in this model?
B) What does the period represent?
C) What does the equation of axis mean in this model?
D) Would a sine or cosine function be more appropriate (if no horizontal translations are applied)? Explain.
Level 4 (Application)
3. A high speed wind turbine, which spins perpendicularly to the ground, is set on a pole that is 35 m tall and completes 5 revolutions in one second.The length of one blade is approximately 1 m long. One particular blade lies parallel to the ground before the turbine started to spin (therefore its initial height was 35 m). What is the equation that models the height of this blade as a function of time?
Key Concepts/Tips
The graphs of sin(x) and cos(x) can model periodic phenomena when they are tranformed to replicate a certain situation. The transformed function is defined as y= asin(k(x-d))+ c and y=acos(k(x-d))+c where the amplitude is calculated by the max - min divided by two the Equation of axis is max + min divided by 2. The period is calculated by the number of cycles usually in 2π and the period is 2π/k. D gives the horizontal translation adand c is the vertical translation or the horizontal axis y = c.
TIP: When modelling a function if the situation starts at a maximum or a minimum point this is a good indicaor to use a cosine function. A sine function can be used and be horizontally translated but using the cosine function is much more convinent.
TIP: When modelling a situation be wary of the k value as well as the period in some cases the situation will not model the period as 2π but as some other number relating to the situation.