
6.1 Radian Measure
Helpful Videos
Converting to and from radians measure.
Example 1
A set of axis can be broken down into four 90 degree angles. It looks like this:
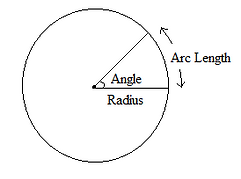
If we were to place a circle on the set of axis, we can coordinate portions of the circle to degrees of an angle. This introduces a new measure called radian. A radian is defined as an angle measured from the center of a circle consisting of an arc that has a length equal to the radius of the circle. Its formula is defined as
θ =a/r.
Confusing right?
How about we forget about the set of axis for a while. Now it’s just a plain old circle.
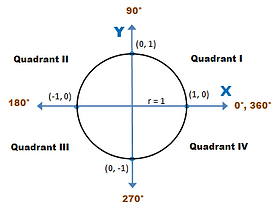
Let’s split up the circle into 4 (like the circle below). We can set the diameter of the circle equal to 1, agreed?
Now substitute the 1 forπ , and it should like the circle in Figure 1 (ignore the terms inside the brackets for now). Instead of π representing only 1, it also represents the angle of a half circle (which is equal to 180 degrees). This is what is known as the unit circle.
In other words, π is equivalent to 180 degrees. So, instead of saying 90 degrees, we can represent the angle as π/2 (180/2 = 90).

IMPORTANT NOTE: Don’t concern yourself with that π symbol. For our purposes, it’s measure in radians is equivalent to the value of 180 degrees.
If you still are struggling with the concept of radian measure, you can think of it like this:
The circumference of a circle is equal to C=2π r.
Since we assume the radius of the unit circle to be 1, than the circumference of the entire circle is instead equal to 2π .
The total angle of a circle must be 360 degrees, which means the angle corresponding to 2π is 360 degrees. Half of 360 degrees, 180, is the angle corresponding to half of 2π , which is π ..
FIG. 1: Unit Circle
So there you have it. That’s all that ugly π symbol represents. Radian measure is simply another way of stating the angle. It is important to practice to become more comfortable with this new measure. Below is a tutorial which demonstrates how to convert between degrees and radian measure, followed by practice questions and helpful links to further your comprehension

Convert each of the following angles to radians or degrees
A) 65° B)2π/3
A) 65°
Step 1) State that and 180 are equivalent.
Step 2) Divide both sides by 180°
Step 3) The 180° now became 1°, and we now can multiply both sides by 65° (multiplied what one degree is equal to by how much degrees we have).
Step 4) Simplify the fraction which is created. You can do this by finding a common factor between 180 and 65, dividing it out. In this case the LCF is 5.
Step 5) Simplify further if you can. If not, express the as an exact value (fraction form) or approx. decimal.
π radians = 180°
π/180 = 180°/180
π/180(65) = (1)(65)
65π/180 = 65°
(π)(65 ÷ 5)/(180 ÷ 5) = 65°
13π/36= 65°
Therefore 13π/36or 1.13 radians = 65°
A) 2π/3
Step 1) State that and 180 are equivalent.
Step 2) Multiply one radian measure by the amount of radians in this case 2/3. Multiply 180 by the same amount (multiplying both sides).
Step 3) Evaluate.
π radians = 180°
(2/3)(π) = (180)(2/3)
2π/3= (180)(2)/3
Therefore2π/ 3radians = 120°
Sample Questions
Level 1/2
Convert Each angle from degrees to radians
a) 90° b) 145 ° c) -255° d) 315°
Convert each angle from radians to degrees
a) 11π/12 b) -3π/6 c) 20π/14 d) 8π/5
Level 3 (Application)
After obtaining 5 stars in the video game GTA V, the swat team sets out to capture your character, destroying anything and everything in their path. A particular helicopter that hovers above shines it’s light (circularly) covering radius 500 m and stops at an angle of 12π24 (relative to its starting point) once it spots your character. Determine the total arc length the spotlight covered while searching for your character.
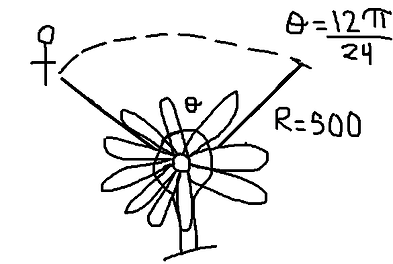
Level 4 (Application)
In an unexpected turn of events, three police officers just committed a robbery. The three squeeze onto a single motorbike with unusually large tires (each having a radius of 80 cm). After an intense chase which lasted about two hours, in which they traveled a total of 100 km, the trio were finally caught. Determine the angular velocity (radians/s) of each tire on the motorbike.
Key Concepts/Tips
Try Out This Game!
Using radians allows you to express the size of an angle as a real number without any units, often in terms of π. It is related to degree measure by the following conversion factor π = 180°
To convert from degrees to radians multiply by π/180°
To convert from radians to degrees multiply by 180°/π