
7.1 Exploring Equivalent Trigonometric Functions
Helpful Videos
Co-function Identities for Angles in the First Quadrant:
1) sin x = cos (π/2 – x) AND cos x = sin (π/2 – x)
2) tan x = cot (π/2 – x) AND cot x = tan (π/2 – x)
3) csc x = sec (π /2 – x) AND sec x = csc (π/2 – x)
Co-function Identities for Angles in the Second Quadrant:
1) sin (x + π/2) = cos x AND cos (x + π/2) = - sin x
2) tan (x + π/2) = - cot x AND cot (x + π/2) = - tan x
3) csc (x + π/2) = sec x AND sec (x + π/2) = - csc x
Use the co-function identities to write an equivalent expression to cosπ/8 and sin5π/12
Example 1
Step 1) Choose a cofunction identity to the sine function so we can start writing an equivalent expression. Since sin[π/2-(x)]=cos we can use this identity to create an expression
Step 2) Plug value into co- function identity and solve.
cosπ/8
cos(x) = sin(π/2 - x )
= sin(π/2 - π/8 )
= sin(4π/8 - π/8)
= sin3π/8
Step 1) Choose a cofunction identity to the sine function so we can start writing an equivalent expression. Since cos[π/2-(x)]=sin we can use this identity to create an expression
Step 2) Plug value into co- function identity and solve.
sin5π/12
sin(x) = cos(π/2 - x )
= cos(π/2 - 5π/12 )
= cos(6π/12 - 5π/12)
= cosπ/12
Using the related acute angle write an expression equivalent to cos7π/8 and sin13π/12
Example 2
Because of their periodic nature, therre are many types of equivalent functions. These equivalent expressions can be checked by using graphing technology to see if both functions overlap perfectly over the entire domain. If this occurs this means that that these expressions are equivalent.
The most basic expressions are equivalent functions of sin(x) and cos(x). The equations y=sin(x-2π) or y=sin(x+2π) y=sin(x+4π) are the same function.
Same goes for cosine functions.Due to their repeating periodic nature, when you shift a full cycle or period, the graph remains the same because it is travelling towards both ends of infinity.These are known as Cofunction identities and are essentially describing complementary angles and (π/2 - x).
Step 1) Determine what quadrant the angle is in and use an identity based on where the angle is. This is 157.5 degrees so in quadrant 2 use the idenity cos(π- x) because if you subtract this from 180 you will get the related acute angle.
cos7π/8 = 157.5 Q(II)
cos(π - x)
cos(π - 7π/8)
cos(8π/8 - 7π/8)
cosπ/8 or 22.5
Check: 180-157.5
=22.5
sin13π/12 = 195 Q(III)
Step 1) Determine what quadrant the angle is in and use an identity based on where the angle is. This is 195 degrees so in quadrant 3 use the idenity cos(π + x)= -cos(x) because the value for cos will be negative due to its location this will add 180
Step 2) This angle is now bigger than 2π or 360 so we will use the identity cos(2π - x) = cos(x) to get the related acute angle
cos(π - x)
cos(π - 7π/8)
cos(8π/8 - 7π/8)
cosπ/8 or 22.5
Check: 180-157.5
=22.5
cos(π + x)
cos(π + 13π/12)
cos(12π/12 + 13π/12)
cos25π/12
cos(25π/12- 2π)
cos (25π12 - 24/12)
cosπ/12 = 15
Check 195 + 180 = 375
375 - 360 = 15

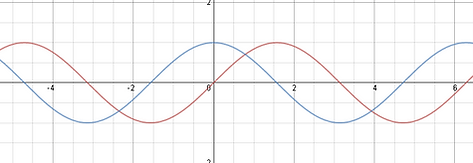
We can use horizontal translations to also make sin(x) and cosine(x) graphs equivalent. Translating the consine function by π/2 to the right is equivalent to the sin(x) function y=cos[(x)+π/2] = y=sin(x) and this means that translating a sin function π/2 to the left makes the sine function equivalent to the cosine function.
The cosine function is an even function so reflecting the graph about the y axis results in an equivalent function cos(x) = cos(-x) This is also true for reciprocal functions sin(x) and tan(x) are odd functions so they posess rotational symmetry about the origin.
Reflecting these functions across both the x-axis and the y-axis produces the same effect as rotating the function through 180 degrees.
sin(-x) = -sin(x) and tan(-x) = tan(x).
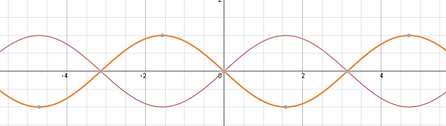
You can also use related acute angles to write equivalent expressions. This can be done by comparing principle angles drawn in standard position in quadrants II, III, and IV with thier related acute angle in quadrant I. The graphs down below are not equivalent since one is a flipped sine graph.
Key Concepts/Tips

Even Function: cos(x) = cos(-x)
Odd Function: sin(-x) = -sin(x) tan(-x)=-tan(x)
Quadrant II
sin (π - x) = sin(x)
cos(π - x) = -cos(x)
tan(π - x) = -tan(x)
Quadrant III
sin (π + x) = -sin(x)
cos(π + x) = -cos(x)
tan(π + x) = tan(x)
Quadrant IV
sin (2π- x) = -sin(x)
cos(2π + x) = cos(x)
tan(2π + x) = -tan(x)
Sometimes you may have to subtract from 360 if your angle becomes greater than 360 degrees, use co functions cooresponding to the quadrant where the angle is located.