
7.3 Double Angle Formulas
Helpful Videos
Simplify the following expression: 2sinπ/6cosπ/6
Evaluate.
Example 1
Step 1) Identify which double angle formula is and the value of a. In this case, the expression matches the double angle formula of sin 2a. This means that a is π/6.
Step 2) Since the expression matches the right side of the double angle formula of sin, we can simplify the expression to the left side of the sin 2a.
sin 2a = 2 sin a cos a
sin 2π/6=2 sin π/6cos π/6
= sin2π/6
= sin π/3
= √3/2
Therefore the expression 2 sinπ/6cosπ/6is equal to √3/2.
Given that cos x =5π13 where 0 x π/2
determine sin 2x.
Step 1) We know that x lies in the first quadrant. We can draw it like in the following diagram. Since we have the hypotenuse and one of the legs, we can easily solve for the other side.
Step 2) Since we know the opposite, adjacent and hypotenuse we now have sin x and cos x.
Step 3) We can sub in these values of sin x and cos x into the sin double angle formula. All that is left is to simplify and we will have determined sin 2x.
cos x =5 π13, therefore 5 = adjacent and 13 = hypotenuse
to solve for opposite:
13^2 - 5^2 = opp^2
169 - 25 = opp^2
144 = opp^2
12 = opp
sin x =O/H cos x =A/H
=5/13 =12/13
sin 2x = 2 sin x cos x
= 2 (5/13)(12/13)
=[(2)(5)(12)]/(13)(13)
= 120/169
Therefore, the exact value of the primary trig ratio of this double angle is 120/169.
In this part of the chapter, we will practice identifying and applying double angle formulas.
What are double angle formulas? Double angle formulas are similar to compound angles as they are also used to calculate exact values. You can also use double angle formulas to simplify expressions.
Instead of breaking up an angle and evaluating it using compound angle formulas, , we are actually identifying the double angle formula and simplifying the expressions to sin 2x, cos 2x or tan 2x.
When we double the value of x, we should get an angle that we can evaluate exactly (see example 1).
This is one strategy we use with double angle formulas. We can additionally use double angle formulas to determine primary trigonometric ratios for unknown angles (see example 2).
The double angle formulas are stated below. Click this link and take a look at pages
2-3 (check out only numbers 2-The double angle formulae for sin 2A, cos 2A and tan 2A and 3-The formula cos 2A = cos2A - sin2A) to see how the double angle formulas are derived
The tutorial below will demonstrate how to manipulate double angle formulas to receive different answers.
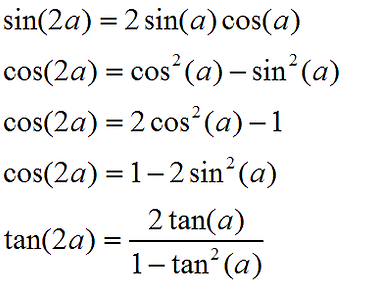
Example 2
Sample Questions
Level 1/2
1. Express each of the following expressions as a single trigonometric ratio.
a) 2 sin 6x cos 6x b) 1 - sin^2(2y)
c) (2 tan)/ (1-tan^2(x)) d) cos^2a - sin^2a
2. Use double angle formulas to rewrite each trigonometric ratios.
a) sin 10t b) cos 3x c) tan 18z d) cos 2p
3. Evaluate these expressions after having expressed each as a single trigonometric ratio.
a) 2 sin 30° cos 30° b) 2 cos^2 π/4 - 1
c) 2 tan(π/12)cos^2(π/12)
Level 3
4. If tan x = (3/-4) where π/2 < x < π what is cos 2x?
Level 4
5. Summarize what you have learned of double angle formulas. Include the unique characteristics of each in order to help you remember how to manipulate them.
Key Concepts/Tips
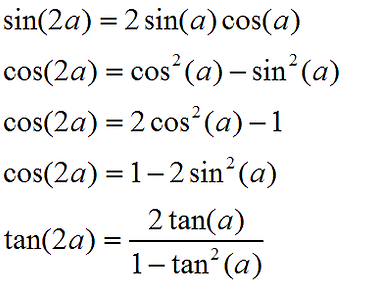
The double angles formulas can be derived from compound angle formulas, we can use these double angle formulae to simplify expressions as well as calculating exact values. Double angle formulas can also be applied when solving identities and are often used to create other equivalent expresssions.
TIPS: It might be useful to know where they are derived because this may help in solving equivalent expressions or identity problems.