
6.2 Radian Measure and Angles On The Cartesian Plane
Helpful Videos
Find the exact value of cos(-7 π/6) and the reciprocal of this trigonometric ratio.
Recall: There are special triangles which are used to calculate the exact values of primary and reciprocal trigonometric ratios. Since reciprocal trigonometric functions are simply 1 over the primary trigonometric ratios, we can easily find their exact values when we know the value of their corresponding primary trigonometric ratio.
In grade 11, we practised using these exact values of trigonometric ratios however with angles measured in degrees. Now, we take it a step forward and attempt to interpret trigonometric ratios with angles in their radian measure.
NOTE: the negative indicates the angle is backwards.
Step 1) Identify the related acute angle and which quadrant it is located in.
The related acute angle is π/6
(In degrees: 7π/6 is equal to 180 plus 30°, the related acute angle must be 30°).
If there was no negative, this angle would be located in the 3rd quadrant (T), but since there is the angle is going clockwise (starting from 0 and going towards 3π/2 instead of how it normally goes to π/2 )
Therefore it’s terminal arm will end in the second quadrant (S) instead.
cos(-7 π/6) = cos(5π/6)
= - cos ( π/6)
= - √3/2
Therefore the exact value of
cos(-7 π/6) is = -√3/2 .
Step 2) Identify the ratio and its sign.
Step 3) Sub in the exact value of cos(-7π/6) and solve for the exact ratio for the reciprocal function.
(x) = -7 π/6)
sec(x) = 1/cos(x)
=1/-√3/2
=1 x -2/√3
= -2/√3
Therefore the exact value of
sec(-7 π/6) is = -2/√3 .
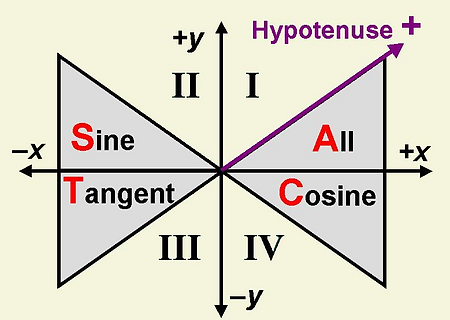
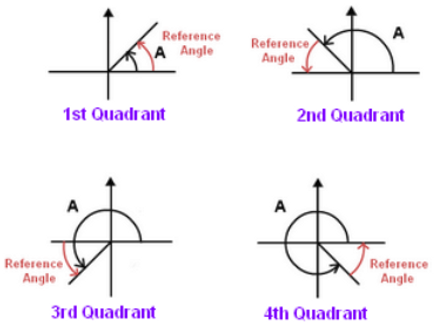
The first step to take when encountered with one of these problems is to translate the angle onto the unit circle. From there, we are able to identify which quadrant the angle is located in and can apply CAST rules (see Figure 2) to determine if the ratio will be positive or negative.
If using radian measure seems a little ominous, feel free to convert the angle from radians into degrees, but make sure to provide the angle in the measure the question required.
After identifying the angle, it is important to realize that we only know exact values of the related acute angles, so we need to find which related acute angle we are dealing with. For example 7π/4 has a related acute angle of π/4 so in order to calculate the cosine of 7π/4 , we are actually looking for the exact value of cos π/4 . This is because the terminal arm of the principal angle is always away from the axises by an amount that is equivalent to the related acute angle (see Figure 3)
Figure 2
Figure 3
Example 1
Sample Questions
Level 1/2
Determine which quadrant each angle is located in. Then determine the sign each angle would have if evaluated for the tan ratio.
a) -8π/9 b)55π/28 c)5π/12 d) 99π100
Determine the exact value of each trigonometric ratio.
a) cos(-5π/4) b) csc(-4π/3) c) cot(11π/6) d) tan(2π/3)
Level 3 (Application)
The Leaning Tower of Pizza forms a triangle between the ground and a 55 m tall tree. The obtuse angle the tower makes on the other side is measured as 5π/6 . If a powerful wind suddenly pushed the Tower so that it was standing straight up, what would its height be?

Key Concepts/Tips
The angles in special triangles can also be expressed in degrees or radians which can then be used to determine the exact values of the trigonometric ratios.
Remember: sin = y/r cos = x/r tan = y/x csc = r/y sec= r/x cot= x/y
CAST Rule:
Quadrant 1 (all positive)
Quadrant 2 (sin positive)
Quadrant 3 (tan positive)
Quadrant 4 (cos positive)