
7.4 Proving Trigonometric Identities
Helpful Videos
Prove the identity:
Example 1
Step 1) Split up the identity into the left side and right side. Since the right side has a denominator that is a binomial, let’s start with that side. We can easily multiply it by its conjugate 1 - cosx and the denominator should become 1 - cos^2x (difference of squares).
Step 2) Continue to simplify the right side. The next approach should be to factor out a sin x from the numerator (since both terms contain a sin x). According to the pythagorean identity, 1 - cos^2x is equal to sin^2x, so we can simplify that to sin^2x.
Step 3) Step 3: Since sin^2x is equal to (sinx)(sinx), we can cancel out the sin x in the numerator and one of the sin x’s on the bottom.
Step 4) Compare the left side to right side. Notice how they are the same? Congratulations! You’ve just proved a trigonometric identity!
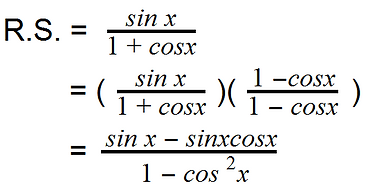
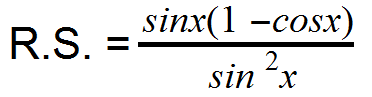

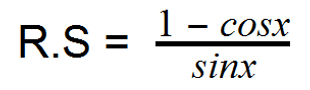
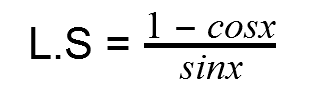
Believe it or not, but you have actually been dealing with trigonometric identities for much of this chapter.
A trigonometric identity is written as an equation, and is simply stating that both sides of the equation are equivalent.
However, a trigonometric identity shouldn’t be treated like how we usually treat equations. Why? Because we aren’t actually trying to solve for anything like how we normally solve equations, so we aren’t actually trying to isolate a variable(no isolating variables, etc.).
Furthermore, that technique where we perform the same operations on both sides of the equation (ie multiplying, dividing, adding, etc.) is not necessarily used. This is because we don’t necessarily really need to(not solving for anything). Ultimately, we are only trying to prove that both sides of the equation are equivalent.
When proving, we deal with both sides of the equation separately, as though each is a separate expression; simplifying the left side, simplifying the right side and then comparing the two.
So what are we doing? Well, a big part of trigonometric identities is simplifying. In fact that’s really all it is. We are simplifying both sides until they look the same.
When proving, we deal with both sides of the equation separately, as though each is a separate expression; simplifying the left side, simplifying the right side and then comparing the two.
There are several tools at your disposal to simplify. Firstly, all the double angle formulas, compound angle formulas and reciprocal trigonometric ratios can be substituted in (or out) when simplifying. Other identities include quotient identities and pythagorean identities. All of these are stated below.
Asides from that you can always expand, which can lead you to recognize anotherother identities or organize other strategies.

IMPORTANT NOTE: the word identity is used to describe the equivalence of two things. Trigonometric identities is stating the equivalence of several oother identities (ie. double angle, pythagorean, etc.) but it is really stating their equivalence.
HELPFUL TIPS and TRICKS
-
It is sometimes suggested to start with the more messier, complicated side first. You may develop another technique when keeping it neater.
-
If it seems helpful, you can completely rewrite both sides of the equation into identities you spot.
-
Use factoring and common denominators whenever it is possible.
-
Turn the 1’s into what you want them to be! It’s tempting to use the pythagorean identity right away, but you can make the 1 into anything, expressing it as an equivalent fraction (ie. cos xcos x).
-
If the denominator is a binomial, try multiplying by conjugates! Since the conjugate can be set to one, it will be as though all you are really doing is multiplying by one. But since the conjugate is the opposite sign, it enables you to cancel some terms out. Click the link below to learn how to use the technique of multiplying by the conjugate.
-
When solving trigonometric identities, things can get messy. To make things easier for yourself, simplify on a scrap piece of paper or on the side and sub back in. This helps keep things neater and you will be able to organize your thoughts easier.
-
Try and convert everything in terms of sine or cosine. You will find it relatively easier to spot other identities and to simplify.
Why would we bother going through all that trouble just to prove two things are equivalent? Well that’s because sometimes trigonometric identities aren’t always true.
Basically, what we are trying to achieve with trigonometric identities is proving that they are true. Other identities, like quotient identities and compound angle, have been proven true, but what about a random combination of these?
That’s up to you to prove. Below is an example that will demonstrate how to apply the techniques and tricks we previously discussed.
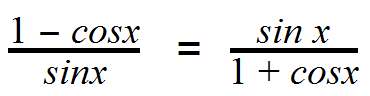
Sample Questions
Level 1/2
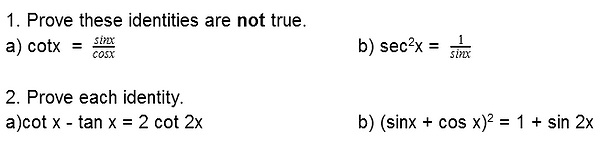
Level 3
3. Explain why we don’t solve trigonometric identities like how we normally solve for equations by describing the definition of an identity.
Level 4
4. Make a chart which summarizes everything you learnt about trigonometric identities. Include examples, tricks, techniques and step by step descriptions of how to prove trigonometric identities.
Key Concepts/Tips

You can also verify idnetities by graphing each side seperately and showing that the are equivalent. To help simplify the identity you can use strategies such as LCD or the lowest common denominator. Identities have an infinite amount of solutions becuase the solution set is in all real numbers in which the expression on both sides of the identity are defined